Monetary Unit Sampling (MUS) is a popular statistical sampling method performed in an audit. One of the crucial, and confusing, parts of MUS is how to select samples. In this post, you’ll learn through examples how to pick samples using three Monetary Unit Sampling selection methods.
Inventory Audit
Say you need to perform the inventory audit on an audit engagement. The auditee gave you the inventory data below. The data will serve as our simple example of a Monetary Unit Sampling application.
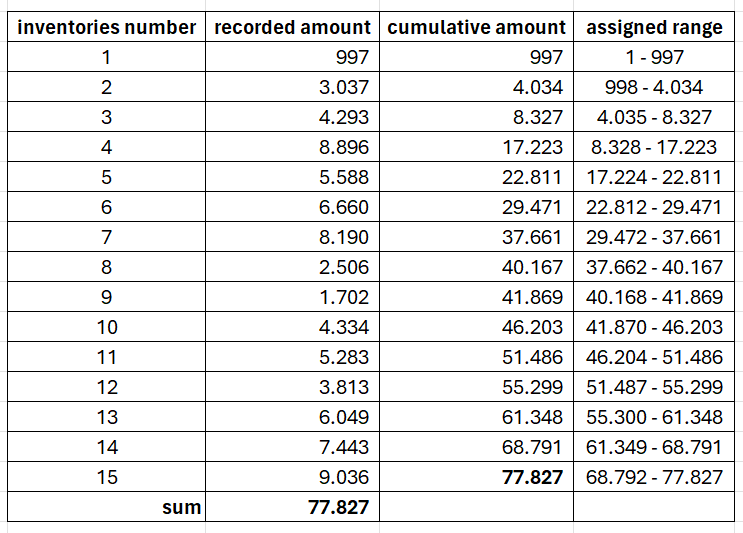
The recorded amount of inventory population size is 77.827, whereas the sample size is 5; thus, you’ll need to pick five logical units. Selecting the sample size is another beast you’ll learn another day. For now, you’ll pick five as the sample size.
Logical Unit is the balance or transaction the auditor examines.
(AICPA Audit Sampling Guide)
You’ll also need to add a cumulative amount column and an assigned range column for each line. Since the process involves selecting a logical unit with a specific number, those two columns provide excellent help.
Monetary Unit Sampling Methods of Item Selection
- Simple Random Sampling
- Systematic Sampling
- Cell Sampling
- Sieve Sampling
- Stabilized Sieve Sampling
- Lahiri Sampling
Above are several sample selection methods in Monetary Unit Sampling. This post will cover the first three as the monetary unit sampling selection examples based on their popularity.
If you are wondering about the definition of MUS and are interested in the method’s history, you can read it here.
Simple Random Sampling in Monetary Unit Sampling Selection
The simple Random Sampling (often abbreviated as SRS) method might be the simplest of all others. You only need to generate five (sample size) random numbers between 1 and 77.827 (population). This can be easily achieved using the RANDBETWEEN function in MS Excel and Google Sheets.
After having five random numbers, pick the logical units whose assigned range column contains the said random number. This time, the process gives you logical unit numbers 15, 4, 7, 6, and 4.
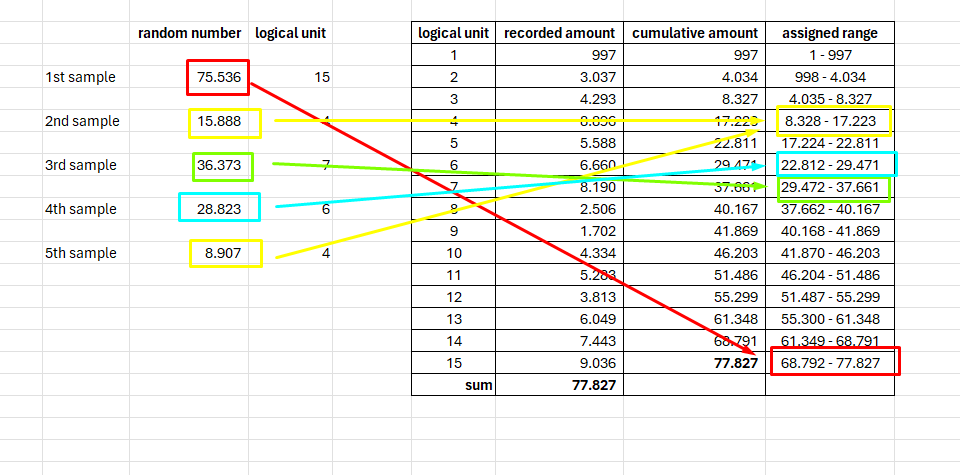
As shown in the image, the 4th logical unit is chosen twice. You don’t need to regenerate the random number because the 4th logical unit will treated as two sample items.
Systematic Sampling in Monetary Unit Sampling Selection
Systematic Sampling also known as Fixed-interval sampling or Systematic selection. This method asks you to get the sampling interval by dividing the population by sample size. If the sample size is five and the population is 77.827, the sampling interval would be 15.565.
For the first sample, you will generate a random number between 1 and 15.565 (the sampling interval). Say you get 935. The second sample is the first sample added by sampling interval, i.e., 16.500 (935 + 15.565). The following sample is the previous sample added by sampling interval.
The process iterates until you get all samples as the sample size needs. The picture below shows that the method picks logical units 1, 4, 7, 11, and 14.
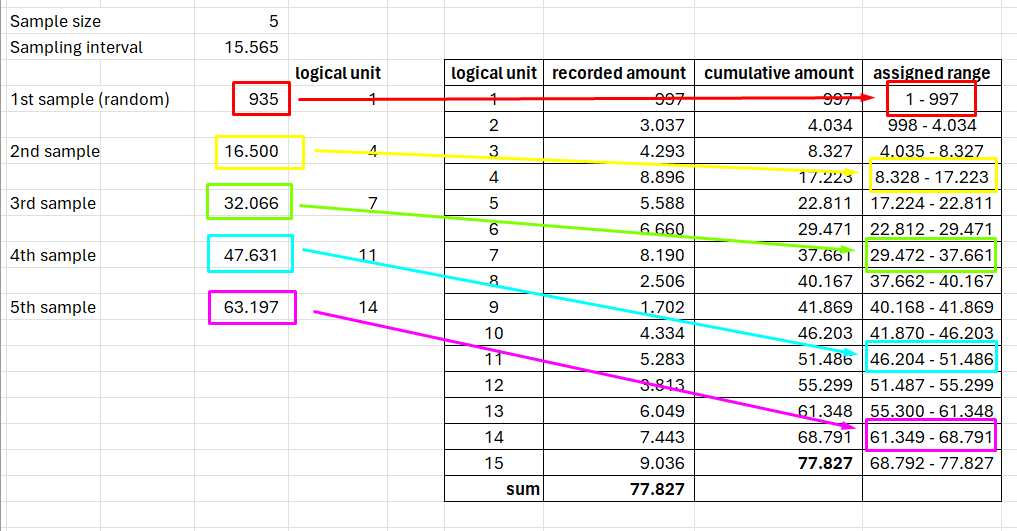
If the logical unit’s recorded amount exceeds the sampling interval, it will be chosen at least once.
As you might think, the rest is automatically chosen after the first sample is picked. This puts the systematic sampling in the possibility of bias if the population’s characteristic is not randomly distributed.
For example, if errors occur at a particular time of the month (or another period), the results from the systematic sampling have a higher chance of failing to be representative of the population.
Cell Sampling in Monetary Unit Sampling Selection
Cell Sampling divides the population into homogenous subgroups or cells. To determine the number of cells, you will base it on the sample size. So, for instance, if your sample size is five, this would imply you will have five cells.
First, you divide the population by the sample size to get the cell’s width. If 77.827 is the population and 5 is the sample size, 15.565 is the cell’s width. This process is similar to getting the sampling interval in systematic sampling.
After getting the cell’s width, you assign each cell’s range. And generate a random number from each range.
The last step is selecting the logical unit to which each cell’s random number points. Using the method, you get the 4th, 6th, 8th, 11th, and 15th logical units as the samples you’ll examine.
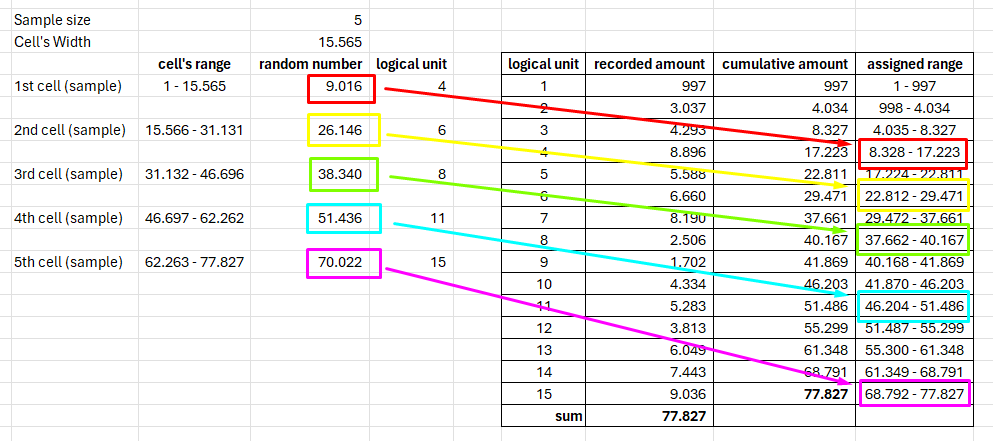
With the cell sampling method, independent selection is made within each interval. That differentiates the technique from the systematic sampling method, thus reducing the possibility of bias.
Cell sampling advantages:
- It’s simple.
- The result is exactly the same as the desired sample size.
- The samples will distributed evenly across the population.
Monetary Unit Sampling Selection, Step-by-Step Examples
Simple Random Sampling
- Get the data.
- Set sample size (n).
- Add a cumulative amount column.
- Add an assigned range column.
- Generate n random numbers between 1 and the population.
- Using the assigned range column, find the logical unit where the random number falls.
Systematic Sampling
- Get the data.
- Set sample size (n).
- Add a cumulative amount column.
- Add an assigned range column.
- Get the sampling interval (k) by dividing population (B) by sample size (n). k = B/n.
- Generate a random number (r) between 1 and k. Use it as the 1st sample.
- Get the n-th sample by adding the previous sample with k. For example: 2nd sample = 1st sample + k; 3rd sample = 2nd sample + k; etc.
- Using the assigned range column, find the logical unit where the sample falls into.
Cell Sampling
- Get the data.
- Set sample size (n).
- Add a cumulative amount column.
- Add an assigned range column.
- Divide the population (B) into n cells. Each cell’s width (k) is the population (B) divided by sample size (n). k = B/n.
- Assign each cell’s range.
- Generate a random number within the specified range for each cell.
- Using the assigned range column, find the logical unit respected to each cell’s random number.
If you are interested in a more statistical perspective of previous sampling methods, give the Horgan thesis a shot; it’s worth reading. For another topic around Monetary Unit Sampling covered in this blog, you can find it here.
Cover Images generated by Canva’s Text to Image App.